Genauigkeit von Prognosen und Hochrechnungen
Was bedeuten Ergebnisse im Kontext?
Hochrechnungen: Ab wann ist „sicher“ wirklich sicher?
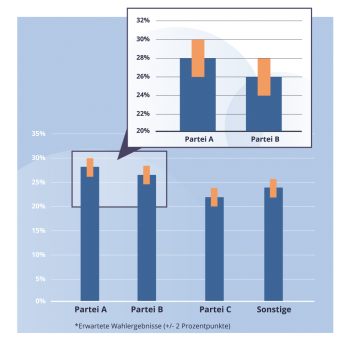
Nina und Markus verfolgen gebannt den Wahlabend im Fernsehen. Bei der dritten Hochrechnung ändert sich plötzlich das Ergebnis: Partei A sinkt von 28 auf 25 Prozent der Stimmen, Partei B steigt von 26 auf 29 Prozent. „Diese Schwankung liegt aber nicht mehr nur bei plus/minus zwei Prozentpunkten“, wundert sich Markus.
Als mögliche Ursache nennt die Nachrichtensprecherin eine höhere Anzahl an Briefwähler*innen bei der diesjährigen Wahl. Das Ergebnis dieser Wählergruppe sei von den verantwortlichen Wahlforscher*innen falsch geschätzt worden, ...

… denn unter den Briefwähler*innen waren deutlich mehr Wähler*innen der Partei B als ursprünglich angenommen. Die Wahlforscher*innen müssen also die wahrscheinlichste Verteilung bei den noch nicht ausgezählten Stimmen berechnen. Unterscheiden sich die bereits ausgezählten Stimmen von den noch nicht ausgezählten erheblich, ist eine genaue Vorhersage nur schwer möglich.
Fazit: Es kommt nicht nur darauf an, ob Daten repräsentativ sind, sondern auch darauf, ob sie eine systematische Verzerrung enthalten.
Exercise:
Wovon hängt die Sicherheit einer Wahlvorhersage ab? Eine Wahlvorhersage ist …
Geht's auch genauer?
Die Schwankungen bei den Wahlprognosen haben Nina und Markus nachdenklich gestimmt. Sie fragen sich, warum die Prognosen in den letzten Jahren immer ungenauer geworden sind. Warum lassen sich starke Schwankungen so schwer vorhersagen?
Bei ihren Recherchen stoßen sie auf die Nachrichtenseite N, die bei der Bundestagswahl tatsächlich korrekte Vorhersagen geliefert hat.

Wie hat die Nachrichtenseite N eine solch genaue Prognose geschafft? Um das herauszufinden, liest sich Nina die Methodenbeschreibung aufmerksam durch:
1. N gewichtet die Wahlumfragen von Prognoseinstitute danach, wie genau deren Vorhersagen in der Vergangenheit gewesen und wie viele Menschen von ihnen jeweils befragt worden sind.
2. Zusätzlich fließen in die Prognosen öffentliche Daten und Trends ein – zum Beispiel, dass sich die Altersverteilung in der Bevölkerung über die Jahre ändert.
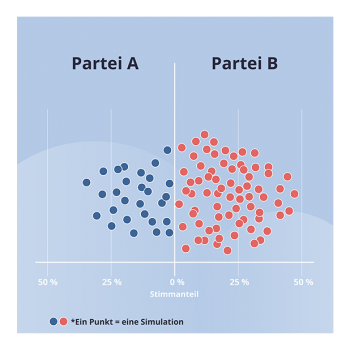
3. Im nächsten Schritt werden Tausende mögliche Wahlausgänge simuliert. Es ist, als würde man ein Spiel viele Male spielen. Dieses Verfahren wird übrigens als Monte-Carlo-Simulation bezeichnet.
4. Am Ende wird überprüft, in wie vielen Durchgängen ein bestimmtes Ereignis – zum Beispiel „Partei A gewinnt die Wahl“ – eingetreten ist. Diese Häufigkeit liegt oft nah an der tatsächlichen Wahrscheinlichkeit. Statistiker*innen sagen, es gilt das „Gesetz der großen Zahl“.